

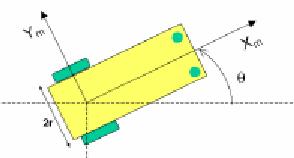
Задача 1. Мобильный робот «Емелина печь-2» имеет два колеса (см. рисунок), а устойчивость сохраняет при помощи волшебной силы. Емеля дал роботу задание: проехать прямо на север на N оборотов колес. К сожалению, ни Емеля, ни робот не знали, что на левом колесе робота спустила шина и оно стало меньше правого на 10%. На сколько метров отклонится правое колесо робота от направления на север, если его радиус R метров, расстояние между колесами D метров, а колеса жестко закреплены на оси и проскальзывание колес отсутствует.
Стандартный математический рецепт поиска точки максимума функции – двигаться по направлению производной (градиента). На практике такая функция часто является представлением физического объекта – скалярного поля, заданного на плоскости или в пространстве. К его примерам относится уровень радиации, концентрация заражающего местность агента, температура горения в зоне пожара и т.п. Часто измерение или оценивание градиента такого поля – сложная задача, в то время как общедоступные датчики измеряют его значение в текущей точке. Поиск экстремума по измерению только значений функции без использования градиента называют неградиентным.
Имеются основания полагать, что с задачей неградиентного поиска экстремума уже миллионы лет неплохо справляются биологические организмы. В частности среди приведенных в
Задача: осмыслить алгоритмическую составляющую интеллектуальных достижений рыб, бактерий и др. биологических организмов в неградиентном поиске экстремума (интеллект студента также приветствуется), предложить математические алгоритмы и проанализировать их поведение, выявив плюсы и минусы.
СПбГУ подписан на ряд журналов, поэтому через сайт библиотеки университета возможно бесплатно получить многие материалы.
В мобильной роботике (от английского robotics, в отечественной лингвистической традиции – робототехнике) под навигацией обычно понимают процедуру поиска пути «из точки A в точку B» в среде, где этот поиск нетривиален. Классический пример – прокладка маршрута на карте. Форма существования карты (на бумаге, в голове навигатора, в памяти компьютера и т.п.) второстепенна, важен априорный доступ к достаточно полным данным о среде. Однако даже таким домашним устройствам, как робот-пылесос, приходится иметь дело с априори неизвестной (роботу) средой. Построение, насколько это возможно, карты «на лету» по результатам сенсорного знакомства со средой – один из разумных путей поиска дееспособных в такой ситуации алгоритмов навигации. Это однако может потребовать значительных вычислительных ресурсов и сенсорных возможностей, а полученное знание среды может быстро терять актуальность в динамических средах. Фактор ресурсов и возможностей приобрел особое значение в связи с ростом интереса к простым, массовым, дешевым и универсальным робототехническим платформам «общего назначения», для которых наряду с целым рядом привлекательных качеств характерны сенсорные, вычислительные, коммуникационные и др. ограничения. В воздушной сфере примером таких платформ могут служить различные компактные квадрокоптеры и дроны.
Реактивная (от английского reactive, одновременно англицизм и биологизм, от «реагирующий на раздражение») навигация --- это навигация, при которой текущие показания датчиков непосредственно преобразуются в текущее управляющее воздействие на мобильный робот в духе мгновенной рефлекторной реакции организма на внешнее раздражение; память и сложные умозаключения или вычисления при этом не используются (либо память используется в мизерной степени). Запрос незначительных ресурсов – очень привлекательная черта реактивных алгоритмов. Основной проблемный момент: можно ли таким образом решать нетривиальные задачи по поиску «глобального» перемещения между двумя удаленными локациями в сложной и неизвестной среде?
Утвердительный ответ был известен еще в древней Греции в виде «правила правой руки» выхода из лабиринта: достаточно перемещаться по нему не теряя контакта правой руки (впрочем, левая рука ничуть не хуже) со стенкой лабиринта и (при неограничительных предположениях о лабиринте) выход будет в конце концов найден. В какой степени этот успех можно перенести на другие задачи, какие именно, каким образом, каковы достоинства и недостатки полученных таким образом алгоритмических решений, где их целесообразно использовать? Эти и другие естественные вопросы не абстрактны, а мотивированы конкретными задачами современной мобильной робототехники.
Сформировавшийся как итог многих проб и ошибок интерес к реактивной навигации роботов вытекает из недавних успехов этого сравнительно молодого направления. В части, касающейся кафедры теоретической кибернетики, многие соответствующие разработки получены в сотрудничестве с Университетом Нового Южного Уэллса (Сидней, Австралия) и отражены в следующих монографиях:
Matveev A.S., Savkin A.V., Hoy M., and Wang C.
Safe Robot Navigation Among Moving and Steady Obstacles
Elsevier, Oxford, UK, 2016, 344 p.
ISBN: 9780128037300
Savkin A.V., Cheng T.M., Xi Z., Javed F., Matveev A.S., Hguyen H.
Decentralized Coverage Control Problems for Mobile Robotic Sensor and Actuator Networks
IEEE Press and John Wiley & Sons, 2015, Hoboken, NJ, 192 p.
ISBN: 978-1-119-02522-1
Дееспособность этих разработок уже подтверждена не только теоремами и компьютерным моделированием, но работающими экспериментальными прототипами коммерческих продуктов.
До последнего времени транспортировка тяжелых пациентов в лечебных учреждениях (даже наиболее развитых) включала перекладывание пациента между стационарными и мобильными койками и физическое перемещение мобильной койки оператором. Здесь возникают проблемы не только с точки зрения быстродействия и эффективности (в отделениях нейрохирургии качественная транспортировка может потребовать до 4 подготовленных специалистов), но и с точки зрения сопутствующих рисков. Эти проблемы особо актуальны в случае пациентов с тяжелыми черепно-мозговыми травмами, где жизненно важно сочетание быстроты с плавным, гладким перемещением, исключающим резкие ускорения.
Вместе с тем общая тенденция к более высокой отдаче и эффективности лечебных учреждений приводит к тому, что обстановка в них становится все более динамичной и малопредсказуемой. Как следствие угрожающий процент осложнений, возникающих при транспортировке пациентов с тяжелыми черепно-мозговыми травмами, вызван человеческим фактором:
U. Beckmann, D. M. Gillies, S. M. Berenholtz, A. W. Wu and P. Pronovost
Incidents relating to the intra-hospital transfer of critically ill patients
Intensive Care Medicine 30(8), 1579--1585 (2004)
Потеря концентрации, усталость, переключение внимания (в том числе, вполне оправданное) и другие несовершенства человеческой природы способны привести к самым трагическим последствиям. Но даже если этого к счастью удалось избежать, время транспортировки (которое также жизненно важно) часто неприемлемо велико:
L. Smith, B. Jordan and J. Paddle
Transfer delays in patients referred for neurosurgical intervention with traumatic brain injury
Critical Care 16(1), 475 (2012)
F. Rincon, S. A. Mayer, J. Rivolta, J. Stillman, B. Boden-Albala, M. S. Elkind, R. Marshall and J. Y. Chong
Impact of delayed transfer of critically ill stroke patients from the emergency department to the neuro-ICU
Neurocritical Care 13(1), 75--81 (2010).
P. Leach, C. Childs, J. Evans, N. Johnston, R. Protheroe and A. King
Transfer times for patients with extradural and subdural haematomas to neurosurgery in greater manchester
British Journal of Neurosurgery 21(1), 11--15 (2007)
C. R. Lind, P. A. Heppner, T. M. Robins and E. W. Mee
Transfer of intubated patients with traumatic brain injury to Auckland city hospital
Australia and New Zealand Journal of Surgery 75(10), 858--862 (2005).
В этом в частности проявляет себя необходимость физического перемещения значительной (для возможностей среднего человека) массы, включая сложное маневрирование с жесткими требованиями к плавности, что часто побуждает оператора делать все медленно.
Одно из перспективных направлений преодоления отмеченных проблем связано с применением моторизованных больничных коек и их автоматизации. Моторизованные койки уже далеко не редкость в лечебных учреждениях. Однако довольно удивительно, что вплоть до последнего времени моторизация касалась в основном адаптации формы и ориентации кровати и ряда вспомогательных функций, но не транспортировки. В качестве одной из причин указанного обстоятельства можно указать на то, что моторизованная транспортировка тяжелых больных делает крайне желательной, вплоть до необходимости, как минимум частичную автоматизацию этой функции с тем, чтобы возросшие возможности по ускорению койки не нанесли вред пациенту. Таким образом, с самого начала вопрос ставится как разработка роботизированного устройства.
Результаты одной из первых в мире практических разработок экспериментального прототипа роботизированной моторизованной койки для транспортировки больных с тяжелыми черепно-мозговыми травмами представлена в работах
Chao Wang, Alexey S. Matveev, Andrey V. Savkin, Ray Clout, and Hung T. Nguyen
A semi-autonomous motorized mobile hospital bed for safe transportation of head injury patients in dynamic hospital environments without bed switching
Robotica (2016) volume 34, pp. 1880--1897.
A.S. Matveev, A.V. Savkin, M.~Hoy, and C.Wang
Safe Robot Navigation Among Moving and Steady Obstacles.
Elsevier, Oxford, UK, 2016, 344 p.
ISBN: 9780128037300
(В работе также участвовали сотрудники Университета Технологии Сиднея.) Видеофайлы некоторых экспериментов: DSCF0036.AVI (113MB), DSCF304.mp4 (33MB). (В экспериментах участвует разработанный мотоблок койки и автономный модуль интеллектуального управления, кровать на мотоблоке не смонтирована, исследовалась способность модуля управления обеспечить уклонение от «непредвиденных» препятствий.) Прилагательное «роботизированный» означает, что на данном этапе речь пока не идет о полном исключении человека из процесса транспортировки. Применяется удаленное телеуправление оператором, а автоматизированный интеллектуальный блок берет управление на себя в ситуации угрозы столкновения с препятствиями.
В экспериментальном прототипе реализованы математические разработки коллектива авторов, касающиеся алгоритмов автономной реактивной навигации в сложных средах с динамическими и статическими препятствиями. В этих разработках принимали участие студенты и аспиранты мат-меха А. Захарьева, А. Анисимов, А. Семакова, К. Овчинников; частично эти разработки отражены в следующих публикациях в ведущих международных журналах в области теории управления и роботики:
Alexey S. Matveev, Hamid Teimoori, and Andrey V. Savkin
Range-only measurements based target following for wheeled mobile robots
Automatica, Volume 47, Issue 1, January 2011, Pages 177-184
Alexey S. Matveev, Hamid Teimoori, and Andrey V. Savkin
Navigation of a unicycle-like mobile robot for environmental extremum seeking
Automatica, Volume 47, Issue 1, January 2011, Pages 85-91
Alexey S. Matveev, Hamid Teimoori, and Andrey V. Savkin
A method for guidance and control of an autonomous vehicle in problems of border patrolling and obstacle avoidance
Automatica, Volume 47, Issue 3, March 2011, Pages 515-524
Michael Hoy, Alexey S. Matveev, Matt Garratt, and Andrey V. Savkin
Collision-free navigation of an autonomous unmanned helicopter in unknown urban environments: sliding mode and MPC approaches
Robotica, Volume 30, Issue 04. July 2012, pp 537-550
A.S. Matveev, C. Wang, and A.V Savkin
Real-time navigation of mobile robots in problems of border patrolling and avoiding collisions with moving and deforming obstacles
Robotics and Autonomous Systems, volume 60, issue 6, year 2012, pp. 769-788
M.C. Hoy, A.S. Matveev, and A.V. Savkin
Collision free cooperative navigation of multiple wheeled robots in unknown cluttered environments
Robotics and Autonomous Systems, volume 60, issue 10, year 2012, pp. 1253-1266
Alexey S. Matveev, Hamid Teimoori, Andrey V. Savkin
Method for tracking of environmental level sets by a unicycle-like vehicle
Automatica 48(9): 2252-2261 (2012)
Michael Hoy, Alexey S. Matveev, Matt Garratt, Andrey V. Savkin
Collision-free navigation of an autonomous unmanned helicopter in unknown urban environments: sliding mode and MPC approaches
Robotica 30(4): 537-550 (2012)
A.S. Matveev, M.C. Hoy, and A.V. Savkin
The problem of boundary following by a unicycle-like robot with rigidly mounted sensors
Robotics and Autonomous Systems, Volume 61, Issue 3, March 2013, Pages 312-–327
A.S. Matveev, M.C. Hoy, and A.V. Savkin
A Method for Reactive Navigation of Nonholonomic Under-Actuated
Robots in Maze-Like Environments, Automatica, Volume 49, Issue 5, May 2013, Pages 1268--1274.
A.S. Matveev, M. Hoy, J. Katupitiyac, and A.V. Savkin
Nonlinear sliding mode control of an unmanned agricultural tractor in the presence of sliding and control saturation
Robotics and Autonomous Systems, Volume 61, Issue 9, September 2013, Pages 973--987
Alexey S. Matveev, Michael Hoy, and Andrey V. Savkin
3D Environmental Extremum Seeking Navigation of a Nonholonomic Mobile Robot
Automatica, Volume 50, Issue 7, July 2014, Pages 1802--1815
Michael Hoy, Alexey S. Matveev, and Andrey V. Savkin
Algorithms for collision-free navigation of mobile robots in complex cluttered environments: a survey
Robotica, Robotica. Vol. 33, Issue 03, March 2015, pp 463-497
A. Zakhar'eva, A.S. Matveev}, M.C. Hoy, A.V. Savkin
Distributed control of multiple non-holonomic robots with sector vision and range-only measurements for target capturing with collision avoidance
Robotica, Volume 33, Issue 02, February 2015, pp 385-412
Alexey S. Matveev, Michael C. Hoy, Andrey V. Savkin
A globally converging algorithm for reactive robot navigation among moving and deforming obstacles
Automatica, Vol.54, 2015, pp.292--304
Kirill S. Ovchinnikov, Anna A. Semakova, and Alexey S. Matveev
Cooperative Surveillance of Unknown Environmental Boundaries by Multiple Nonholonomic Robots
Robotics and Autonomous Systems, Volume 72, October 2015, Pages 164--180.
A.S. Matveev, M.C. Hoy, K.S. Ovchinnikov, A. Anisimov, and A.V. Savkin
Robot navigation for monitoring unsteady environmental boundaries without field gradient estimation
Automatica, Volume 62, 2015, pp. 227--235.
A.S. Matveev, M.C. Hoy, and A.V. Savkin
Extremum Seeking Navigation Without Derivative Estimation of a Mobile Robot in a Dynamic Environmental Field
IEEE Transactions on Control Systems Technology, Volume 24, Issue 3, 2015, pp. 1084--1091
A.S. Matveev, A.A. Semakova, and A.V. Savkin
Range-only based circumnavigation of a group of moving targets by a non-holonomic mobile robot
Automatica, Volume 65, 1 March 2016, Pages 76--89
A.A. Semakova, K.S. Ovchinnikov, and A.S. Matveev
Self-deployment of mobile robotic networks: an algorithm for decentralized sweep boundary coverage
Robotica, DOI: 10.1017/S0263574716000539, Published online: 09 August 2016, Pages 1-29
Есть робот футболист, цель которого – подъехать к мячу с нужной стороны и ударить по мячу в направлении ворот. Считается, что роботу в каждый момент времени известны координаты на плоскости мяча, ворот и робота, а также угол направления движения робота. Необходимо написать алгоритм, в каждый момент времени по известным величинам вычисляющий необходимую угловую и линейную скорость движения робота (они обе ограничены по модулю). Этот алгоритм должен за конечное время привести робота к мячу с заданной стороны (в направлении удара мяча по воротам).

Задача имеет много способов решения различной сложности. Предлагается предложить хотя бы один.